앞서 정리한 Simple Linear Regression을 구하기 위한 Gradient Descent 알고리즘을 좀 더 세세하게 정리하고 이를 TensorFlow로 구현하자.
Hypothesis함수와 cost함수를 아래와 같이 정의했었다.

Gradient Descent 알고리즘을 간단히 확인하기 위해 b를 생략하여 함수를 간략화했다.

이 간략화한 함수의 개형을 확인하기 위해 x, y 데이터는 y=x그래프 위의 데이터를 사용하고 W 값을 변화시켜 costt함수의 값의 변화를 확인하면

목표가 cost가 최소가 되는 W값을 찾는 것이었다. 해당 결과에서 W=1 일 때 cost가 최소인 것을 확인할 수 있다.
이걸 기계가 찾는 알고리즘이 Gradient descent이며, 경사를 따라 내려가면서 최저점을 찾도록 설계된 알고리즘이다. 엔지니어링 문제의 대부분은 최적화 문제이며 이 최적화 문제는 이득을 최대화시키거나 손실을 최소화하는 방법을 찾는 것 손실을 최소화 즉, cost를 최소화하는 방법으로 널리 쓰이는 게 바로 Gradient descent이다.
위에서는 Weight값을 4개 정도로 변화시켜 cost값의 변화를 계산했다. 해당의 방법을 사용하여 W값의 변화에 대하여 cost함숫값의 변화를 그래프로 확인하면 다음과 같다.

해당 그래프에서 cost가 최저점이 되는 곳을 눈으로는 쉽게 찾을 수 있지만 기계가 찾을 수 있도록 하기 위해 Gradient descent알고리즘을 사용한다.

[Gradient descent 동작 과정]
1. 최초 추정을 통해서 W와 b의 값을 정한다(0, 0이나 랜덤 값 상관없다.) W와 b 값을 Cost가 줄어들 수 있는 방향으로 조금씩 줄어들도록 W와 b의 값을 지속적으로 바꾼다.
2. W와 b값을 지속적으로 업데이트할 때 기울기 값을 구해서 Cost가 최소화되는 방향으로 업데이트를 해나간다.
3. 해당 과정 반복
4. 최소점에 도달했다고 판단될 때까지 반복
W값에 따라 변화하는 파란색 선인 cost함수를 확인한다. 임의의 점 W=4의 기울기를 구하고 W값에 Gradient를 곱해서 W 값에서 빼준다. Gradient가 양수이기 때문에 Weight가 이동을 하게 된다. 새로운 지점에서 과정을 반복하면 언젠가는 기울기가 굉장히 작은 지점에 도착한다. 기울기가 0이 되면 더 이상 Weight의 변화가 생기지 않기 때문에 해당 지점이 cost가 최소화되는 지점이다. W가 마이너스인 부분에서 시작해도 기울기가 음수라 W가 증가하기 때문에 같은 지점에서 정지하게 된다. 기울기가 클수록 많이 움직이고 지점에 다가갈수록 기울기가 작기 때문에 조금씩 움직인다.
이때 gradient를 미분을 통해 구한다. 따라서 cost함수를 미분해야 한다.

미분하기 전에 계산의 편의를 위해 함수를 수정하자, 나누는 수는 평균을 위해 점의 개수를 사용하는 것이기 때문에 m, 2m, 4m 등 개수는 cost값에 영향을 미치지 않는다. 따라서 미분할 때 앞으로 나오는 지수를 없애기 위해 2m을 사용하자.

Weight 값을 지속적으로 업데이트하는 내용이다.
이 값에 따라 변화의 정도가 결정된다. 주로 다양한 변화를 확인하기 위해 0.01, 0.0001처럼 작은 값 사용한다.
cost함수를 W에 대해 미분하고 W에서 그 값을 빼주고 W에 assign 한다. 이때 W에 대한 편미분을 수행한다.
W란 지점에서의 기울기 값에 특정한 상수만큼 곱해서 W에서 뺀다 그리고 다시 W에 업데이트한다. 얼마나 많이, 빠르게는 알파에 의해 결정된다. 따라서 알파는 학습을 얼마만큼 할지, 즉 W값을 얼마만큼 변경할지를 결정하는 파라미터가 된다. 이 알파를 learning rate, 학습률이라고 한다.

cost함수와 미분을 통한 W의 업데이트를 정리하면 위와 같다.

이때 주의할 점은 시작 위치에 따라 가장 낮은 지점을 찾지 못할 수도 있다. 주변에서 가장 낮은 지점 local minimum의 존재 때문에 전체 중에 가장 최저점이라고 보증할 수 없다. 즉 이런 상황에서는 사용할 수 없다.

따라서 Gradient descent알고리즘은 로컬 미니멈과 글로벌 미니멈이 일치하는 convex함수일 때 사용할 수 있다.
구현
cost function in pure python)
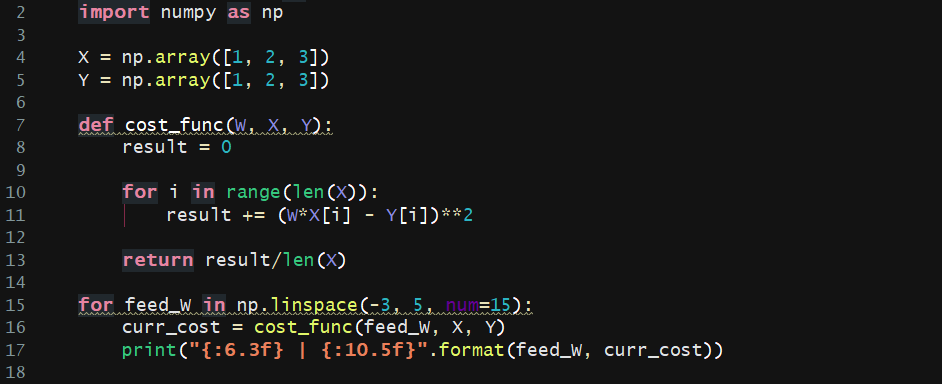

cost 함수를 파이썬으로만 작성할 경우 위와 같다.


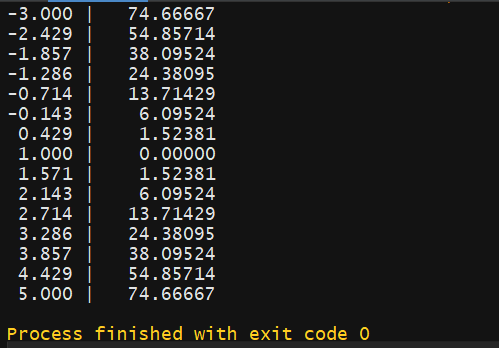
위와 같은 cost함수의 구현을 위해 우선 주어진 데이터만큼 반복문을 수행 (W*x-Y)**2 의 결과를 result 변수에 누적하고 값을 반환할 때 개수만큼 나누어 평균값을 반환한다. W값을 -3~5 의값중 15개를 사용하기 위해 linspace(시작, 끝, 개수) 함수를 사용하여 cost_func에 인수로 전달하여 W값에 따른 cost함수를 확인할 수 있다. 앞에 개념과 같은 데이터를 사용했기 때문에 동일하게 W=1에서 최소 cost인 0을 가지는 2차 함수 모양의 그래프를 따른다.
cost function in tensorflow)
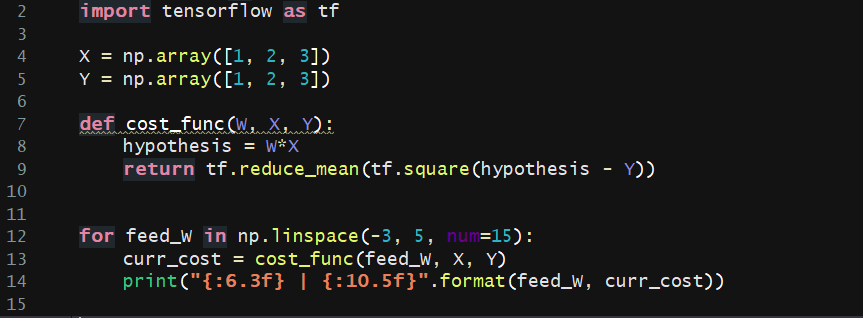
tensorflow를 사용하여 cost함수를 구현할 경우 앞의 정리에서 사용했던 hypothesis 변수와 reduce_mean, square를 사용하는 것 말고는 크게 차이가 없다.
Gradient descent)

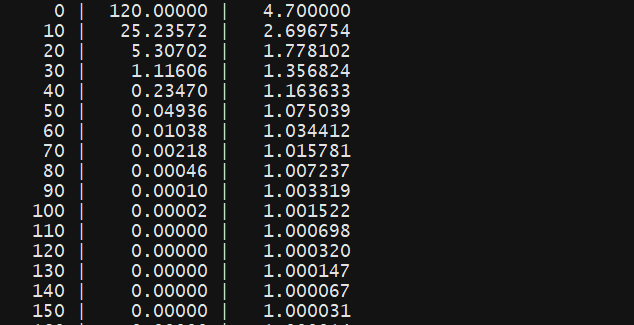
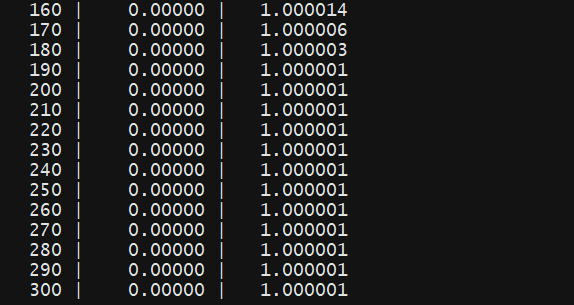
cost함수와 Gradient descent 알고리즘을 사용하여 최종적으로 cost가 최소가 되는 W값을 찾아가는 과정이다.
앞서 정리한 알고리즘의 동작 과정을 수행하기 위해 반복문을 수행하며 매번 기울기에 따라 W값을 assign함수를 통해 업데이트해나가며 cost가 최소가 될 수 있도록 줄여 나간다. 위의 코드에서는 W=5일 때 점에서 수행했다.

W에 random.normal()을 사용하여 -100~100 사이의 임의의 값이 들어가도록 하여 수행하여도 동일한 결과를 얻을 수 있다.



댓글